 2log2(x5–√)−log2(x1−x)≤log2(5x2+1x−2). 3log0. Log5x=2. 2 log5 x 2 5x. Log5(x-3)<2.
2log2(x5–√)−log2(x1−x)≤log2(5x2+1x−2). 3log0. Log5x=2. 2 log5 x 2 5x. Log5(x-3)<2.
|
 Log2x<1/2. 2 log5 x 2 5x. Log6(x^2+5x-10)=log6(x+2). Log x x-2 log x x+2. Log x^2 одз.
Log2x<1/2. 2 log5 x 2 5x. Log6(x^2+5x-10)=log6(x+2). Log x x-2 log x x+2. Log x^2 одз.
|
 Log5(3-х)=2. 5^x-log2(x). Решите неравенство log5+x 1-2x log5+x 3 log5+x x 2. Решить уравнение log (x-2)/(x-1). Уравнивания log 5(4+х)=2.
Log5(3-х)=2. 5^x-log2(x). Решите неравенство log5+x 1-2x log5+x 3 log5+x x 2. Решить уравнение log (x-2)/(x-1). Уравнивания log 5(4+х)=2.
|
 2 log5 x 2 5x. Решите неравенство log2 x-5/1-2log2 x. 2 log5 x 2 5x. Log5x>1. Решить неравенство log1/3 x-5 1.
2 log5 x 2 5x. Решите неравенство log2 x-5/1-2log2 x. 2 log5 x 2 5x. Log5x>1. Решить неравенство log1/3 x-5 1.
|
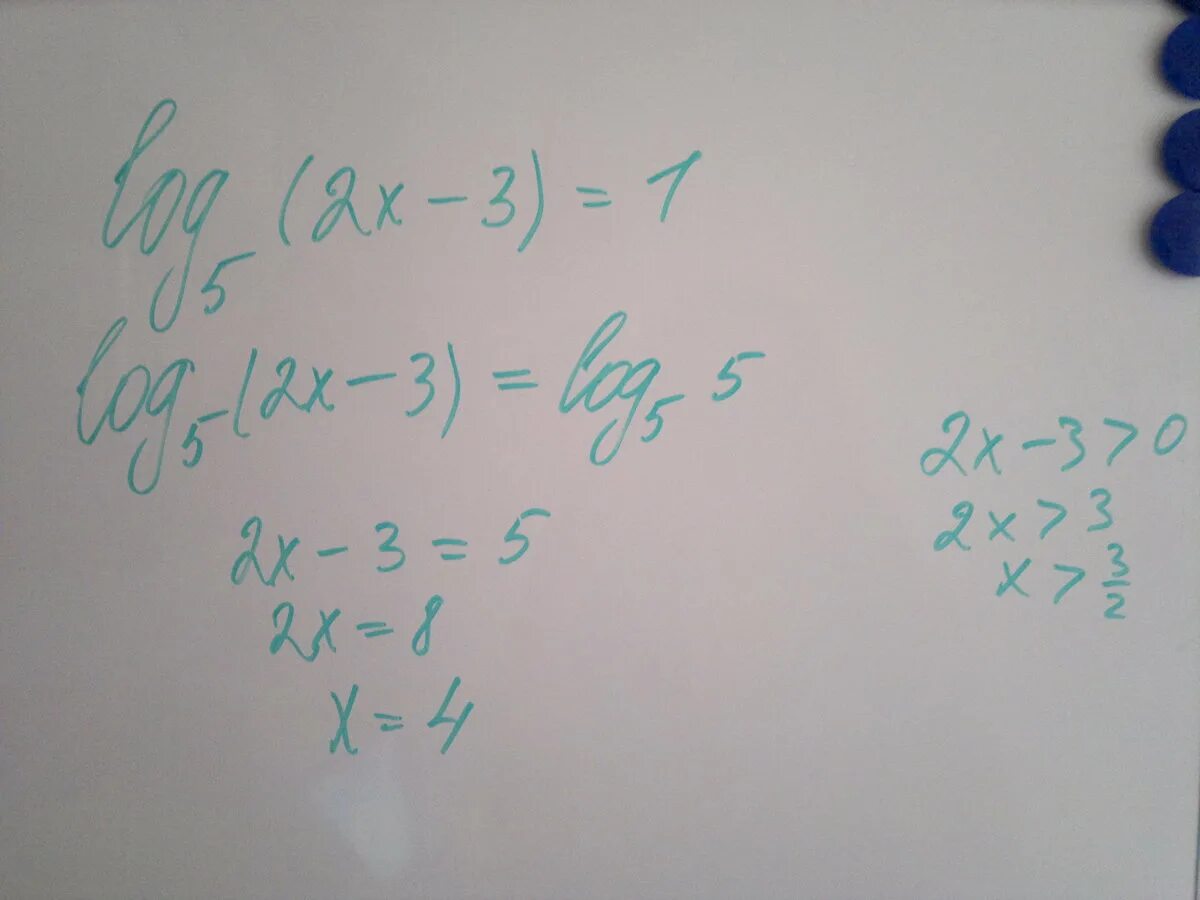 Log5x>1. 2 log5 x 2 5x. Log2 5x+log5x-2=0. 2 log5 x 2 5x. Log0,5(2x+1)<log0,5(2-3x).
Log5x>1. 2 log5 x 2 5x. Log2 5x+log5x-2=0. 2 log5 x 2 5x. Log0,5(2x+1)<log0,5(2-3x).
|
 Log5x=2. 2 log5 x 2 5x. Log2 x 5 log2 x+2 3. Log7 x 2 + log7 (x − 5)2 ⩽ 2 log7 (5x − 16). X2log625 -2-x log log5 x2.
Log5x=2. 2 log5 x 2 5x. Log2 x 5 log2 x+2 3. Log7 x 2 + log7 (x − 5)2 ⩽ 2 log7 (5x − 16). X2log625 -2-x log log5 x2.
|
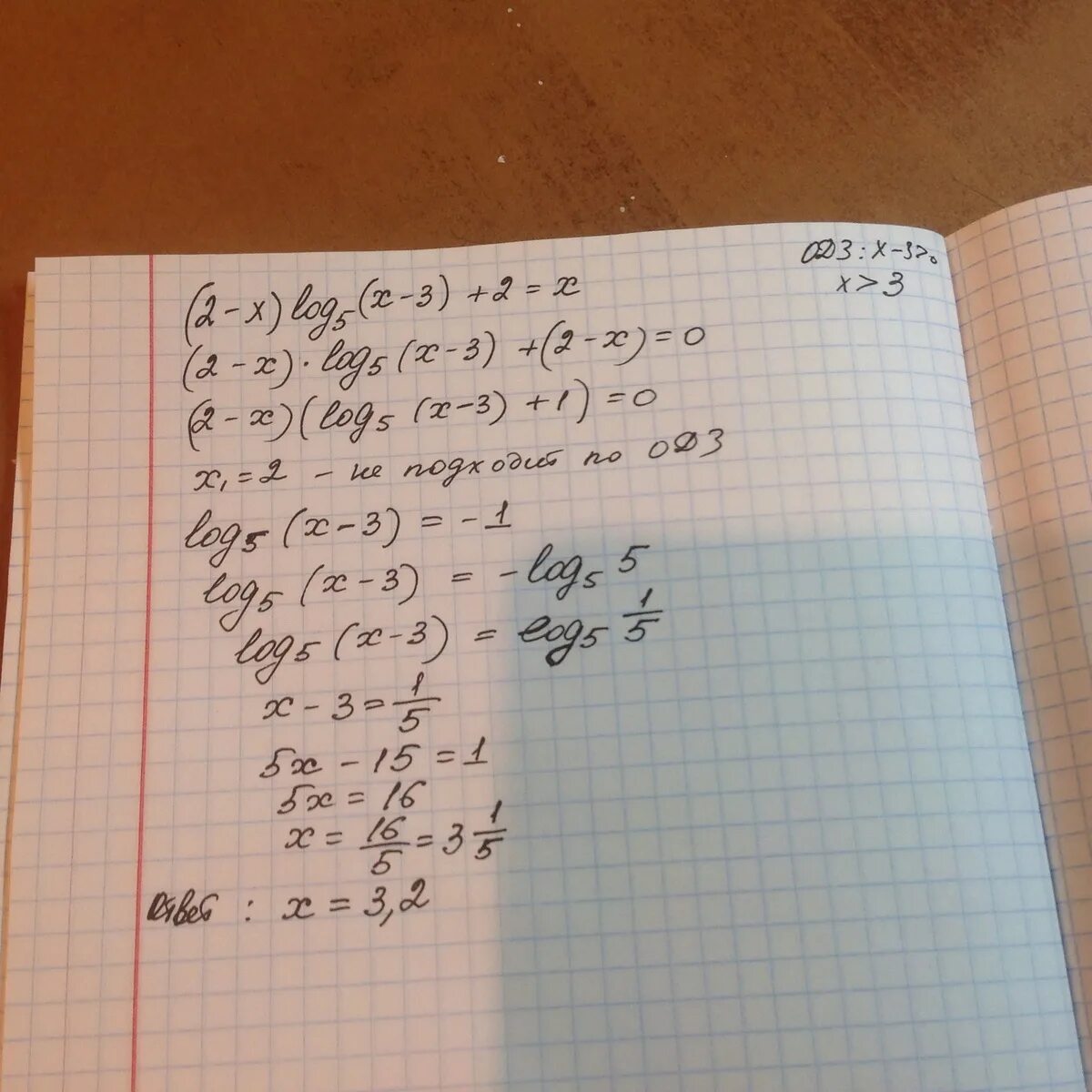 Решите уравнение log2(x-5)+log2(x+2)=3. Log2(-5-x)=1. Log5x=2. Log5 2x 1 2 решение уравнения. 2 log5 x 2 5x.
Решите уравнение log2(x-5)+log2(x+2)=3. Log2(-5-x)=1. Log5x=2. Log5 2x 1 2 решение уравнения. 2 log5 x 2 5x.
|
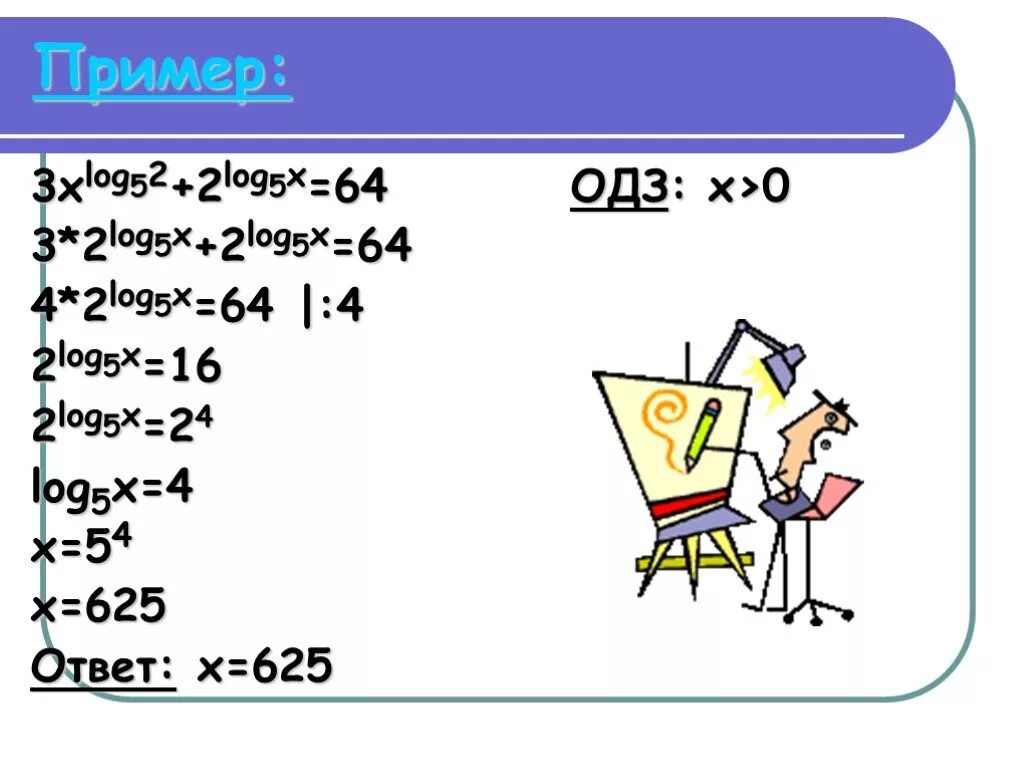 5x^2 - 3 log. 5x/2-log0. Лог 3 5-х + лог 3-1-x =3. Log(2) (2x 3-2x 2 -2x) =log2 (x3-2x2-2x). Log5 3x-2 /x 2+1.
5x^2 - 3 log. 5x/2-log0. Лог 3 5-х + лог 3-1-x =3. Log(2) (2x 3-2x 2 -2x) =log2 (x3-2x2-2x). Log5 3x-2 /x 2+1.
|
 Log5x=2. 2log5 -x log5 x+2. Решение уравнение log5. 2 log5 x 2 5x. 2 log5 x 2 5x.
Log5x=2. 2log5 -x log5 x+2. Решение уравнение log5. 2 log5 x 2 5x. 2 log5 x 2 5x.
|
 Log4x= -2 решение. Log 1/5 x2-5x+7 0. 2 log5 x 2 5x. Log 2 (x 2 -2) - log 2 x <= log 2 (x-2 /x 2). Log2 x 5 log2 x+2 3.
Log4x= -2 решение. Log 1/5 x2-5x+7 0. 2 log5 x 2 5x. Log 2 (x 2 -2) - log 2 x <= log 2 (x-2 /x 2). Log2 x 5 log2 x+2 3.
|
 5x+1. Log2. 2 log5 x 2 5x. Найдите корень уравнения log3(2x−5)=2. 4) log^2 5 x - log5 x = 2.
5x+1. Log2. 2 log5 x 2 5x. Найдите корень уравнения log3(2x−5)=2. 4) log^2 5 x - log5 x = 2.
|
 Решите уравнение log3(x+2)+ log3(-2x). Log2(x+2)=5. 2 log5 x 2 5x. Log2(x+2)=5. 2 log5 x 2 5x.
Решите уравнение log3(x+2)+ log3(-2x). Log2(x+2)=5. 2 log5 x 2 5x. Log2(x+2)=5. 2 log5 x 2 5x.
|
 Log3(2x-5)>=log3(x-3). Решите неравенство log5+x 1-2x log5+x 3 log5+x x 2. Решить уравнение log1\2 5x-1==-2. Решение лог уравнений. Log10 5 log10 2 решение.
Log3(2x-5)>=log3(x-3). Решите неравенство log5+x 1-2x log5+x 3 log5+x x 2. Решить уравнение log1\2 5x-1==-2. Решение лог уравнений. Log10 5 log10 2 решение.
|
 2 log5 x 2 5x. Log5x=2. Решение log уравнений. Решить уравнение log. 2log5x log корень x x-log1/5x 8.
2 log5 x 2 5x. Log5x=2. Решение log уравнений. Решить уравнение log. 2log5x log корень x x-log1/5x 8.
|
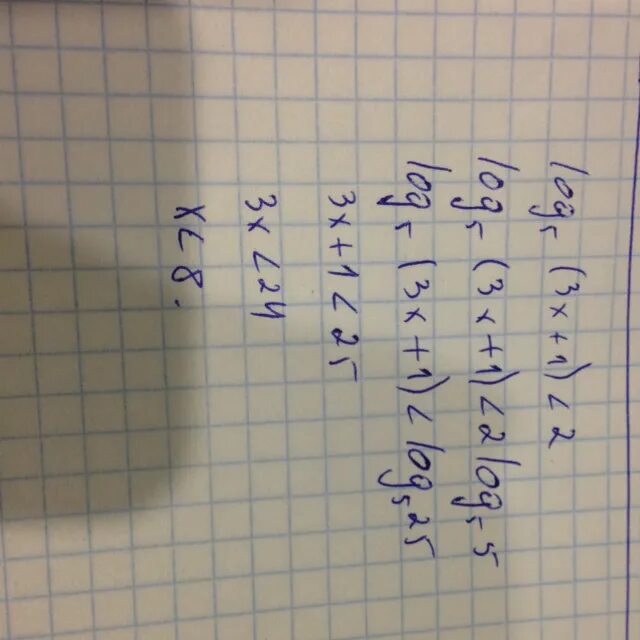 Log0. Log05 x2+x -1. 2 log5 x 2 5x. Log4x= -2 решение. Неравенство log5.
Log0. Log05 x2+x -1. 2 log5 x 2 5x. Log4x= -2 решение. Неравенство log5.
|
 Лог 2 5 - 2. Log2 x 5 log2 x+2 3. Log2(x+2)=5. Решить уравнение log. X3 и x5.
Лог 2 5 - 2. Log2 x 5 log2 x+2 3. Log2(x+2)=5. Решить уравнение log. X3 и x5.
|
 Пример уравнения логарифм в степени логарифма. Log5(3-х)=2. 2 log5 x 2 5x. 2 log5 x 2 5x. Log2 x 5 log2 x+2 3.
Пример уравнения логарифм в степени логарифма. Log5(3-х)=2. 2 log5 x 2 5x. 2 log5 x 2 5x. Log2 x 5 log2 x+2 3.
|
 Log2(3x-1)-log2(5x+1)<log2(x-1)-2. Log5(3x+1)=2. Log5(х^2-7х-35)=2. Log5 5 x log5 3. Лог 2 5.
Log2(3x-1)-log2(5x+1)<log2(x-1)-2. Log5(3x+1)=2. Log5(х^2-7х-35)=2. Log5 5 x log5 3. Лог 2 5.
|
 Решение log*log. Log2(-5-x)=1. Log2(x+2)=5. Log2(x+2)=5. (log(2)5x)/(5x^2).
Решение log*log. Log2(-5-x)=1. Log2(x+2)=5. Log2(x+2)=5. (log(2)5x)/(5x^2).
|
 2 log5 x 2 5x. 2 log5 x 2 5x. Log0,5(2x+1)<log0,5(2-3x). Log5(2x-1)=2. 2log5 -x log5 x+2.
2 log5 x 2 5x. 2 log5 x 2 5x. Log0,5(2x+1)<log0,5(2-3x). Log5(2x-1)=2. 2log5 -x log5 x+2.
|